Terbaru - Bank Soal: Perbandingan Trigonometri Dan Pembahasan

Berikut ini adalah Soal dan Pembahasan Perbandingan Trigonometri yaitu salah satu sub materi TRIGONOMETRI bidang studi Matematika Wajib Kelas 10.

Soal No. 1

Pada segitiga PQR di bawah ini, $\sin \beta $ = …

(A) $\fracpq$
(B) $\fracpr$
(C) $\fracrq$
(D) $\fracqp$
(E) $\fracrp$

$\sin \beta =\frac\textsisi\,\textdepan\textsisi\,\textmiring=\fracqp$
Jawaban: D

Soal No. 2

Pada segitiga KLM di bawah ini nilai dari $\sin \alpha +\sin \beta $ = …

(A) $\frac1210$
(B) $\frac1410$
(C) $\frac1610$
(D) $\frac1810$
(E) $\frac2010$

$\beginalign \sin \alpha +\sin \beta &=\fracMLKL+\fracKMKL \\ &=\frac810+\frac610 \\ \sin \alpha +\sin \beta &=\frac1410 \endalign$
Jawaban: B

Soal No. 3

Jika $\sin \alpha =\frac1213$, dengan $\alpha $ lancip maka $\cos \alpha $ = ….
(A) $\frac1312$
(B) $\frac135$
(C) $\frac513$
(D) $\frac125$
(E) $\frac512$

$\sin \alpha =\frac1213=\fracdemi$
$\beginalign sa &=\sqrtmi^2-de^2 \\ &=\sqrt13^2-12^2 \\ &=\sqrt169-144 \\ &=\sqrt25 \\ sa &=5 \endalign$
$\cos \alpha =\fracsami=\frac513$
Jawaban: C

Soal No. 4

Jika $\cos A=\frac23$, dengan A lancip maka $\tan A$ = …
(A) $\frac13\sqrt5$
(B) $\frac32$
(C) $\frac25\sqrt5$
(D) $\frac12\sqrt5$
(E) $\frac35\sqrt5$

$\cos A=\frac23=\fracsami$
$\beginalign de &=\sqrtmi^2-sa^2 \\ &=\sqrt3^2-2^2 \\ &=\sqrt9-4 \\ de &=\sqrt5 \endalign$
$\tan A=\fracdesa=\frac\sqrt52$
Jawaban: D

Soal No. 5

Jika $\tan A=3$, dengan A lancip maka $\sin A$ = ….
(A) $\frac13\sqrt10$
(B) $\frac810\sqrt10$
(C) $\frac103\sqrt10$
(D) $\frac310\sqrt10$
(E) $\frac110\sqrt10$

$\tan A=3=\frac31=\fracdesa$
$\beginalign mi &=\sqrtde^2+sa^2 \\ &=\sqrt3^2+1^2 \\ &=\sqrt9+1 \\ mi &=\sqrt10 \endalign$
$\beginalign \sin A &=\fracdemi \\ &=\frac3\sqrt10 \\ &=\frac3\sqrt10\times \frac\sqrt10\sqrt10 \\ \sin A &=\frac310\sqrt10 \endalign$
Jawaban: D

Soal No. 6

Bila $0^\circ < a < 90^\circ $ dan $\tan a=\frac5\sqrt11$, maka $\sin a$ = …
(A) $\frac56$
(B) $\frac2536$
(C) $\frac16\sqrt11$
(D) $\frac536$
(E) $\frac136\sqrt11$

$\tan a=\frac5\sqrt11=\fracdesa$
$\beginalign mi &=\sqrtde^2+sa^2 \\ &=\sqrt5^2+(\sqrt11)^2 \\ &=\sqrt25+11 \\ &=\sqrt36 \\ mi &=6 \endalign$
$\sin a=\fracdemi=\frac56$
Jawaban: A

Soal No. 7

Pada gambar disamping nilai $\cos \angle BAC$ adalah ….

(A) $\frac1540$
(B) $\frac1525$
(C) $\frac1520$
(D) $\frac2025$
(E) $\frac2540$

$\beginalign AC &=\sqrtAB^2-BC^2 \\ & =\sqrt25^2-15^2 \\ & =\sqrt625-225 \\ & =\sqrt400 \\ AC &=20 \endalign$
$\cos \angle BAC=\fracACAB=\frac2025$
Jawaban: D

Soal No. 8

Jika $\cos x=2\sin x$, nilai $\sin x\cos x$ adalah …
(A) $\frac15$
(B) $\frac14$
(C) $\frac13$
(D) $\frac25$
(E) $\frac23$

$\beginalign \cos x &=2\sin x \\ \frac12 &=\frac\sin x\cos x \\ \tan x=\frac12 &=\fracdesa \endalign$
$\beginalign mi &=\sqrtde^2+sa^2 \\ & =\sqrt1^2+2^3 \\ mi &=\sqrt5 \endalign$
$\beginalign \sin x\cos x &=\fracdemi\times \fracsami \\ & =\frac1\sqrt5\times \frac2\sqrt5 \\ \sin x.\cos x &=\frac25 \endalign$
Jawaban: D

Soal No. 9

Apabila $4\cot x=3$ dengan sudut $x$ lancip maka nilai dari $\frac\sin x-\cos x\sin x+\cos x$ = ….
(A) $-\frac17$
(B) 0
(C) $\frac17$
(D) $\frac73$
(E) $\frac37$

$4\cot x=3\Leftrightarrow \cot x=\frac34$
$\beginalign\frac\sin x-\cos x\sin x+\cos x &=\frac\frac\sin x\sin x-\frac\cos x\sin x\frac\sin x\sin x+\frac\cos x\sin x \\ & =\frac1-\cot x1+\cot x \\ & =\frac1-\frac341+\frac34 \\ \frac\sin x-\cos x\sin x+\cos x &=\frac17 \endalign$
Jawaban: C

Soal No. 10

Perhatikan gambar berikut!

Diketahui $\Delta ABC$ siku-siku di B, $\cos \alpha =\frac1213$, dan $\tan \beta =1$. Jika$AD=a$, maka $AC$ = …
(A) $\frac12a$
(B) $\frac117a$
(C) $\frac127a$
(D) $\frac137a$
(E) $2a$

Perhatikan segitiga CBD:
$\beginalign \cos \alpha &=\frac1213 \\ \fracABAC &=\frac1213 \endalign$
$\beginalign BC &=\sqrtAC^2-AB^2 \\ &=\sqrt13^2-12^2 \\ BC &=5 \endalign$
$\beginalign \tan \beta &=1 \\ \fracBCBD &=1 \\ BC&=BD=5 \endalign$
$\beginalign AB &=AD+BD \\ 12 &=a+5 \\ a &=7 \endalign$
$\beginalign AC &=13 \\ &=\frac137\times 7 \\ AC &=\frac137a \endalign$
Jawaban: D

Soal No. 11

Jika $\sin x=k$, maka $\frac1-\tan ^2x1+\tan ^2x$ = ….
(A) $1+k$
(B) $1+k^2$
(C) $1+2k^2$
(D) $1-2k^2$
(E) 1

$\beginalign \sin x &=k \\ \fracdemi &=\frack1 \\ sa &=\sqrtmi^2-de^2 \\ sa &=\sqrt1-k^2 \endalign$
$\tan x=\fracdesa=\frack\sqrt1-k^2$
$\tan ^2x=\frack^21-k^2$
$\beginalign \frac1-\tan ^2x1+\tan ^2x &=\frac1-\frack^21-k^21-\frack^21-k^2 \\ &=\frac\frac1-k^2-k^21-k^2\frac1-k^2+k^21-k^2 \\ \frac1-\tan ^2x1+\tan ^2x &=1-2k^2 \endalign$
Jawaban: D

Soal No. 12

Jika $\tan \alpha =-p$ dengan $\alpha $ sudut lancip maka $\sin \alpha $ = …
(A) $\frac-2p\sqrtp^2+1$
(B) $\frac-p\sqrtp^2+1$
(C) $\fracp\sqrtp^2+1$
(D) $\frac2p\sqrtp^2+1$
(E) $\frac1\sqrtp^2+1$

$\beginalign \tan \alpha &=-p \\ \fracdesa &=\frac-p1 \\ mi &=\sqrtde^2+sa^2 \\ &=\sqrt(-p)^2+1^2 \\ mi &=\sqrtp^2+1 \endalign$
$\sin \alpha =\fracdemi=\frac-p\sqrtp^2+1$
Jawaban: B

Soal No. 13

Jika $0 < x < \frac\pi 2$ dan $x$ memenuhi persamaan $6\sin ^2x-\sin x-1=0$, maka $\cos x$ = ….
(A) $\frac2\sqrt33$
(B) $\frac\sqrt32$
(C) $\frac\sqrt23$
(D) $\frac\sqrt33$
(E) $\frac\sqrt34$

Misal:
$\sin x=p$ maka:
$\beginalign 6\sin ^2x-\sin x-1 &=0 \\ 6p^2-p-1 &=0 \\ (3p+1)(2p-1) &=0 \endalign$
$\beginalign p &=-\frac13 \\ \sin x &=-\frac13 \endalign$ atau $\beginalign p &=\frac12 \\ \sin x &=\frac12 \endalign$
Karena $0 < x < \frac\pi 2$ maka yang memenuhi adalah:
$\beginalign \sin x &=\frac12 \\ \fracdemi &=\frac12 \\ sa &=\sqrtmi^2-de^2 \\ &=\sqrt2^2-1^2 \\ sa &=\sqrt3 \\ \cos x &=\fracsami=\frac\sqrt32 \endalign$
Jawaban: B

Soal No. 14

Apabila $\tan \theta =\frac1\sqrt7$ maka nilai dari $\frac\csc ^2\theta -\sec ^2\theta \csc ^2\theta +\sec ^2\theta $ adalah ….
(A) $\frac112$
(B) $\frac37$
(C) $\frac34$
(D) $\frac57$
(E) $\frac43$

$\beginalign \frac\csc ^2\theta -\sec ^2\theta \csc ^2\theta +\sec ^2\theta &=\frac\frac1\sin ^2\theta -\frac1\cos ^2\theta \frac1\sin ^2\theta +\frac1\cos ^2\theta \\ &=\frac1-\tan ^2\theta 1+\tan ^2\theta \\ &=\frac1-\left( \frac1\sqrt7 \right)^21+\left( \frac1\sqrt7 \right)^2 \\ &=\frac1-\frac171+\frac17 \\ &=\frac68 \\ \frac\csc ^2\theta -\sec ^2\theta \csc ^2\theta +\sec ^2\theta &=\frac34 \endalign$
Jawaban: C

Soal No. 15

Apabila $\tan A=t$ dengan A sudut lancip, maka $\sin A$ = ….
(A) $1+t^2$
(B) $1-t^2$
(C) $\sqrt\frac1t^2+1$
(D) $\sqrtt^2+1$
(E) $\sqrt\fract^2t^2+1$

$\beginalign \tan A &=t \\ \fracdesa &=\fract1 \\ mi &=\sqrtde^2+sa^2=\sqrtt^2+1 \\ \sin A &=\fracdemi \\ &=\fract\sqrtt^2+1 \\ \sin A &=\sqrt\fract^2t^2+1 \endalign$
Jawaban: E

Soal No. 16

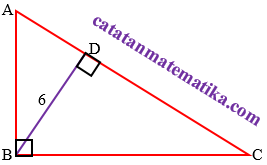
Pada segitiga ABC siku-siku di B dengan $\cos C=\frac13$. Jika BD adalah garis tinggi pada sisi AC dan BD = 6 cm, maka panjang AC = … cm.
(A) $4\sqrt2$
(B) $\frac272\sqrt2$
(C) $5\sqrt2$
(D) $\frac112\sqrt2$
(E) $6\sqrt2$

 
Perhatikan segitiga BDC:
$\beginalign \cos C &=\fracCDBC \\ \frac13 &=\fracCDBC \\ BC &=3CD \endalign$
Teorema pythagoras:
$\beginalign BC^2 &=BD^2+CD^2 \\ (3CD)^2 &=6^2+CD^2 \\ 9CD^2 &=36+CD^2 \\ 8CD^2 &=36 \\ CD^2 &=\frac368=\frac92 \\ CD &=\frac3\sqrt2 \endalign$
$\beginalign BC &=3CD \\ &=3.\frac3\sqrt2 \\ BC &=\frac9\sqrt2 \endalign$
Perhatikan segitiga ABC:
$\beginalign \cos C &=\fracBCAC \\ \frac13 &=\frac\frac9\sqrt2AC \\ AC &=\frac27\sqrt2=\frac272\sqrt2 \endalign$
Jawaban: B

Soal No. 17

Perhatikan gambar berikut!

Nilai $\sin \theta $ dari segitiga di atas adalah …
(A) $\fracbc$
(B) $\fracac$
(C) $\fracba$
(D) $\fraccd$
(E) $\fracca$

$\sin \alpha =\frac\textsisi\,\textdepan\texthipotenusa=\fracac$
Jawaban: B

Soal No. 18

Diketahui sin A = $\fracpq$ dengan $0^\circ < A < 90^\circ $ maka nilai dari $\cos ^2A$ = ….
(A) $\fracp^2p^2+q^2$
(B) $\fracp^2p^2-q^2$
(C) $\fracq^2p^2-q^2$
(D) $\fracq^2+p^2q^2$
(E) $\fracq^2-p^2q^2$

$\sin A=\fracpq=\fracdemi$
$sa=\sqrtmi^2-de^2=\sqrtq^2-p^2$
$\beginalign \cos ^2A &=\left( \fracsami \right)^2 \\ &=\left( \frac\sqrtq^2-p^2q \right)^2 \\ \cos ^2A &=\fracq^2-p^2q^2 \endalign$
Jawaban: E

Soal No. 19

Diketahui nilai $\tan \alpha =\frac13$ untuk $0^\circ < \alpha < 90^\circ $. Nilai dari $2\sin \alpha .\cos \alpha $ = …
(A) $\frac35$
(B) $\frac25$
(C) $\frac15$
(D) $-\frac25$
(E) $-\frac35$

$\tan \alpha =\frac13=\fracdesa$
$\beginalign mi &=\sqrtde^2+sa^2 \\ &=\sqrt1^2+3^2 \\ mi &=\sqrt10 \endalign$
$\beginalign 2\sin \alpha .\cos \alpha &=2.\fracdemi.\fracsami \\ &=2.\frac1\sqrt10.\frac3\sqrt10 \\ &=\frac610 \\ 2\sin \alpha .\cos \alpha &=\frac35 \endalign$
Jawaban: A

Soal No. 20

Diketahui nilai dari $\sin 25^\circ =p$. Nilai dari $\tan 25^\circ $ = …
(A) $\sqrt1-p^2$
(B) $\sqrt1+p^2$
(C) $\fracp\sqrt1-p^2$
(D) $\fracp\sqrt1+p^2$
(E) $\frac2p\sqrt1+p^2$

$\sin 25^\circ =p\Leftrightarrow \fracdemi=\fracp1$
$sa=\sqrtmi^2-de^2=\sqrt1-p^2$
$\tan 25^\circ =\fracdesa=\fracp\sqrt1-p^2$
Jawaban: C

Bagikan Artikel ini